Construction of a novel family of shape-preserving subdivision schemes

By prof. Jungho Yoon
Department of Mathematics
PURE Research Profile
yoon@ewha.ac.kr

• Introduction: What is subdivision
Subdivision is a research area mainly studied in computer graphics, geometric modeling, animation, and computational geometry. It focuses on methods for generating smooth curves and surfaces by repeatedly refining a coarse polygonal mesh. This technique allows artists to work with simple control meshes while achieving high-quality smooth surfaces at render time. Subdivision is widely used across multiple industries, including Pixar, Disney, DreamWorks, and Major VFX Studios. Figure 1 is a 3D model of the Volkswagen Beetle created using the CAD software Rhinoceros 3D (Rhino), developed by Robert McNeel & Associates, It demonstrates a process of subdivision surface modeling.

Figure 1. Beetle 1966: https://www.rhino3d.com/fr/features/subd/#&gid=1&pid=20

• Motivation and Objective
Subdivision schemes provide local control over the shapes of the final limit curves and surfaces. When dealing with a subdivision scheme, along with the convergence and smoothness of the limit function, it is often essential to preserve the fidelity of data (such as monotonicity and convexity) in the limit. Such schemes prevent distortion and undesirable artifacts that may arise with non-shape preserving algorithms during the refinement process, ensuring that the final limit curves and surfaces maintain certain desirable properties. However, many subdivision schemes fail to preserve geometrically significant shapes such as convexity and monotonicity within the given data. Even, most of the existing shape preserving schemes are algorithmically more involved than non-shape preserving schemes. Furthermore, imposing shape preserving constraints often leads to a loss of accuracy or smoothness. In fact, the accuracy and shape preserving property have a rather conflicting relationship, because the loss of monotonicity or convexity with a high-order accuracy is a universal phenomenon in many numerical algorithms. In view of the aforementioned discussion, the objective of this study is to present a novel class of shape preserving subdivision schemes.

• Results
We first devise a techique, namely modified minmod method, to suppress spurious oscillations in vicinity of rapidly changing regions. The proposed minmod technique is then combined with the well-known cubic B-spline scheme to improve its order of accuracy, while retaining the shape preserving property. The resulting subdivision scheme is shape preserving maintaining both monotonicity and convexity of the given initial data, whereas many of the existing schemes focus on either monotonicity or convexity. Moreover, our scheme works regardless of whether the data is strictly or non-strictly convex or monotone. This distinguishes it from the majority of shape preserving algorithms, which are often designed to handle only strictly convex or/and monotone data that satisfies specific, limited conditions. We also provide a rigorous proof that the proposed scheme is third-order accurate and generates C2 limit functions. In addition, the scheme is algorithmically simple to implement. The following figures shows the shape preserving performance of the proposed scheme.

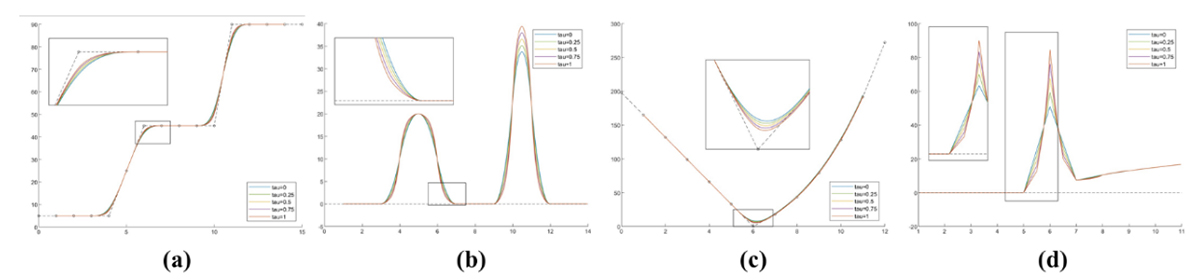
Figure 2. (a) Monotone data (b) The 1st derivative (c) Convex data (d) The 2nd derivative

* Related Article
Yejin Kim, Hyoseon Yang, Jungho Yoon, Shape-preserving subdivision scheme with the third-order accuracy and C2 smoothness, Mathematics and Computers in Simulation, 235, 160-174, 2025