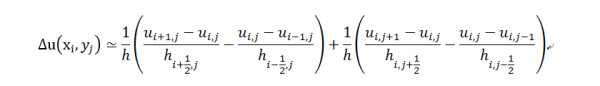본문
Analyses on the finite difference method by Gibou et al. for Poisson equation
by Prof. Chohong Min (chohong@ewha.ac.kr)
Many of natural and social phenomena are described by partial differential equations. The Poisson equation takes the central role among the equations. The finite difference method introduced by Gibou et al. in 2002 is one of the best algorithms to approximate the unknown solution of the Poisson equation; see figure 1. The method is simple and has been observed to produce a second-order accurate numerical solution and a first-order accurate numerical gradient in numerous examples. The method has been conjectured to possess the convergence property in general domains. However many the tried examples are, they are merely finite, which is insufficient to conclude the property true in general.
In this work, we introduced a first and complete mathematical analysis that proves the approximation order of the method by Gibou. Also we estimate the condition number of the linear system associated with the method. The condition number of a linear system is defined as the ratio of the largest eigenvalue to the smallest. A large condition number not only delays the convergence of an iterative matrix solver but also make some of the significance digits disappear. The linear system has quite a large condition number O(1/(h*hmin)), where h is the default step size of the uniform grid of the finite difference method and hmin is the minimum distance between grid nodes and irregular boundary. Due to the large condition number, the linear system needs be preconditioned in order to reduce the condition number.
Gustafsson in 1978 proposed a conjecture that only the MILU preconditioner lessons the size order of the condition number among all the ILU-type preconditioners. His conjecture was proved by Li et al in 2003 when the domain is rectangular. We are the first to confirm his conjecture in irregular domains with the method by Gibou. Our estimation shows that the MILU preconditioner give O(1/h) condition number, while the other ILU-type preconditioners give O(1/(h*h)).
Through our analysis, the method can be now guaranteed to have the convergence order in general. Such guarantee is important in practice especially in real-time simulations and large-sized computations such as weather forecast and computer graphics in move industry. Another contribution of our work is the suggestion of solving the linear system. In three dimensional simulations, the linear system would involve a huge matrix whose size is about one million by one million. In many practices, the linear system has been preconditioned by Jacobi, ILU, or a hybrid of ILU and MILU preconditioner. Our analysis clearly shows that the pure MILU should be used. Our previous work indicated that a parallel computation of the MILU preconditioner is possible. The MILU-preconditioned conjugate gradient with the parallel implementation makes a state-of-the-art algorithm for solving the Poisson equation.
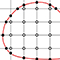
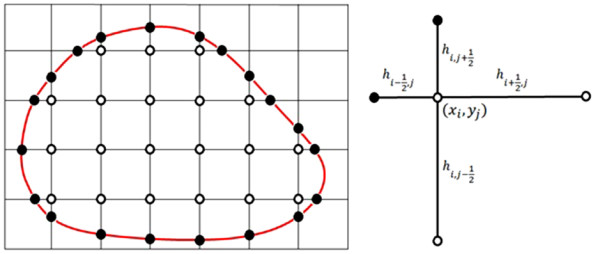
Figure 1. Grid nodes of Ωh are marked by ○ and the nodes of Γh by ●. Each grid node (xi,yj )∈Ωh has four neighboring nodes in Ωh∪Γh in two dimensions. The finite difference method by Gibou et al. approximates the Laplace operator as
The method has more advantages over the standard central finite difference method, the Shortley-Weller method, for it results in a symmetric positive-definite matrix.
* Related Article
Analyses on the finite difference method by Gibou et al. for Poisson equation
Gangjoon Yoon and Chohong Min, Journal of Computational Physics, Volume 280, 1 January 2015, Pages 184-194